Fintokeiで使えるエリオット波動インジケーター3選｜リアルトレードでの使い方も解説！

エリオット波動は、相場の価格変動を一定の波のパターンとして捉えて値動きを予測する相場分析理論として多くのトレーダーに知られています。

「どのトレンドがエリオット波動のどの波に該当するのか？」

「この波のカウントは本当にあっているのか？」

リアルタイムでエリオット波動の波を正しく数えることは難しく、上記のような疑問を持ったことがある方も多いのではないでしょうか？

エリオット波動でお悩みの方に向いているのが、エリオット波動に関連したインジケーターの活用です。

あくまで目安ではあるものの、インジケータを使えばエリオット波動の波を自動でカウントしてくれるので波の数え方に関する悩みを軽減できます。

この記事では、エリオット波動の基本概念から、波のカウントの難しさ、そしてその課題を解決するインジケーターの活用方法まで、以下の項目で詳しく解説します。

• エリオット波動とは？
• エリオット波動を正しくカウントすることは難しい
• インジケーターでエリオット波動のカウント問題が解決
• エリオット波動のインジケーターのカウントは信頼できるのか？
• エリオット波動のインジケーターをトレードで活用する方法
• エリオット波動を使ってFintokeiに挑戦する
• まとめ

エリオット波動とは？

エリオット波動とは、相場で現れる価格変動をパターン化し、「価格の波」のサイクルとして捉えて、今後の相場動向を分析する理論です。

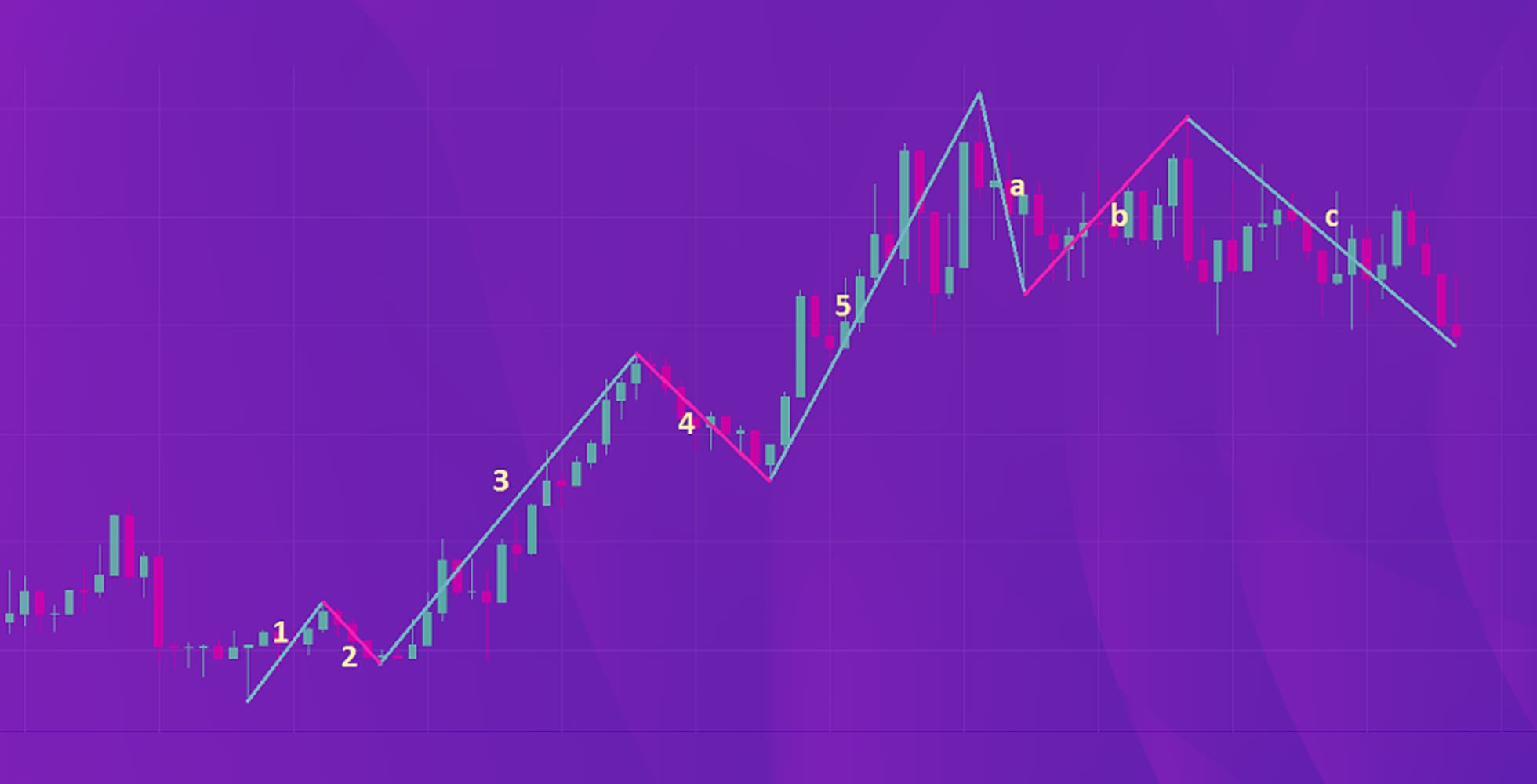
エリオット波動では、相場の価格動向は、5つの推進波と3つの修正波、合計8つの波で構成されるということが基本理論として提唱されています。

たとえば上昇トレンドの場合、上昇中に現れる5つの推進波と、上昇トレンドの終了を示す3つの修正波が現れることで、1サイクルの上昇トレンドが終了します。

さらに推進波には、以下のような原則もあり、この原則を満たすことで、エリオット波動の波としてカウントがされます。

• エリオット波動の第1波は第3波より長くなることがない
• 第1波の安値は第2波の安値を必ず下回る
• 第1波の高値は第4波の安値を必ず下回る

エリオット波動を正しくカウントすることは難しい

価格の波を正しくカウントできるかどうかが、エリオット波動を使いこなせるかどうかを大きく左右します。

しかし実際の相場では正しく波をカウントすることは難しく、エリオット波動は使えない相場分析理論だと言われることも少なくありません。

カウントが難しい代表例として挙げられるのが、第1波です。

以下のチャートを見てみると、安値から一時的に上昇した部分（黄色枠）、または相場価格が大きく上昇した部分（赤色枠）のどちらを1波として捉えるか迷う方もいるのではないでしょうか？

さらに進んだチャートを見ると、結果的に黄色枠のカウントが正しかったことがわかります。

また以下のような暴落相場では、いつ第1波が発生して、上昇トレンドに転換するのか予測するのは難しいのです。

このように、リアルタイムで波をカウントすることは意外と難しく、エリオット波動を使いこなすためにはトレードスキルや経験がある程度必要になるのです。

エリオット波動は使えないのかについては、以下の記事で詳しく解説しているのでぜひ参考にしてください。

≫エリオット波動は本当に使えない？6つの理由と対策方法を徹底解説

インジケーターでエリオット波動のカウント問題が解決

波動のカウントには少しトレードスキルや経験が必要となるエリオット波動ですが、インジケーターを使えば、その問題を解決できる可能性があります。

以下の画像は、チャートにエリオット波動における波を自動でカウントしてくれるインジケーターを適用しただけのものです。

波が自動的にカウントされるので、「どの波が第1波動なのか？」などと悩むことがありません。

エリオット波動に慣れておらず、波のカウントに自信がない場合は、積極的にインジケーターを導入していくと良いでしょう。

Fintokeiで使えるエリオット波動関連のインジケーター

Fintokeiのトレーディングプラットフォームで使えるエリオット波動関連のインジケーターとして、以下の3つを解説します。

• トレーディングプラットフォームに標準で搭載されている「ZigZag」
• 自動で波をカウントしてくれる「Elliot-Wave」
• カウントとフィボナッチを表示する「Elliot-Fibonacci」

※なお、Elliot-WaveとElliot-FibonacciはFintokeiが提供しているインジケーターではないので、別途外部からダウンロードする必要があります。

トレーディングプラットフォームに標準で搭載されている「ZigZag」

ZigZag（ジグザグ）とは、チャート上の目立った安値と高値を結んで、相場の流れを「ジグザグ」に表示するインジケーターです。

ZigZagでは、小さな値動きを無視して大きな流れのみをラインで結んでくれるので、エリオット波動を形成する8つの波を視覚的に把握するために適しています。

また、エリオット波動関連のさまざまなインジケーターの基礎にもなっているインジケーターなので信頼性は高いです。

しかし、波が実際にカウントされるわけではないので、エリオット波動のために使うとなると、ある程度のトレードスキルは必要になります。

カウントも自動化したいという方は、次に紹介する2つのインジケーターから選んでみると良いでしょう。

ZigZagの使い方については、以下の記事で詳しく解説しているのでぜひ参考にしてください。

≫ZigZagのおすすめ設定値とは？目的別にパラメーターを変更するコツも解説！

自動で波をカウントしてくれる「Elliot-Wave」

Elliot-Waveは、エリオット波動の波を自動でカウントしてくれる最もスタンダードなインジケーターです。

ZigZagをベースに作られており、推進波である第1波〜第5波までを自動でカウントしてくれます。

インジケーターのパラメーターはZigZagとほとんど同じなので、まずZigZagを理解しておくと使いこなしやすいインジケーターだといえるでしょう。

ただし、修正波まではカウントされないので、あくまで補助的に活用することがおすすめです。

カウントとフィボナッチを表示する「Elliot-Fibonacci」

Elliot-Fibonacciは、エリオット波動における波のカウントに加えて、フィボナッチツールも表示してくれるインジケーターです。

エリオット波動とフィボナッチの関係性は深く、エリオット波動の「波の終点」や「波の押し目・戻り」を推測するためにフィボナッチ比率はよく活用されます。

このインジケーターでは、価格がどこまで伸びそうかのターゲット価格が表示されるので、利益確定位置やトレンド転換点の把握も自動化できるのです。

またトレンドラインも表示されるので、トレンド方向も一目で理解できる点も特徴です。

ただし、パラメーターの設定項目が文字化けしているので、設定を細かく変更したい方にとっては使いづらいインジケーターとなるでしょう。

エリオット波動とフィボナッチの関係性については、以下の記事で詳しく解説しているのでぜひ参考にしてください。

≫エリオット波動とフィボナッチの関係性を徹底解説！重要な数値やトレードでの使い方とは

エリオット波動のインジケーターのカウントは信頼できるのか？

インジケーターを使って波のカウントを自動化する際に気になるのが、「インジケーターがするカウントは本当に正しいのか？」という点でしょう。

結論として、インジケーターのカウントが正しくない場面がもちろんあります。

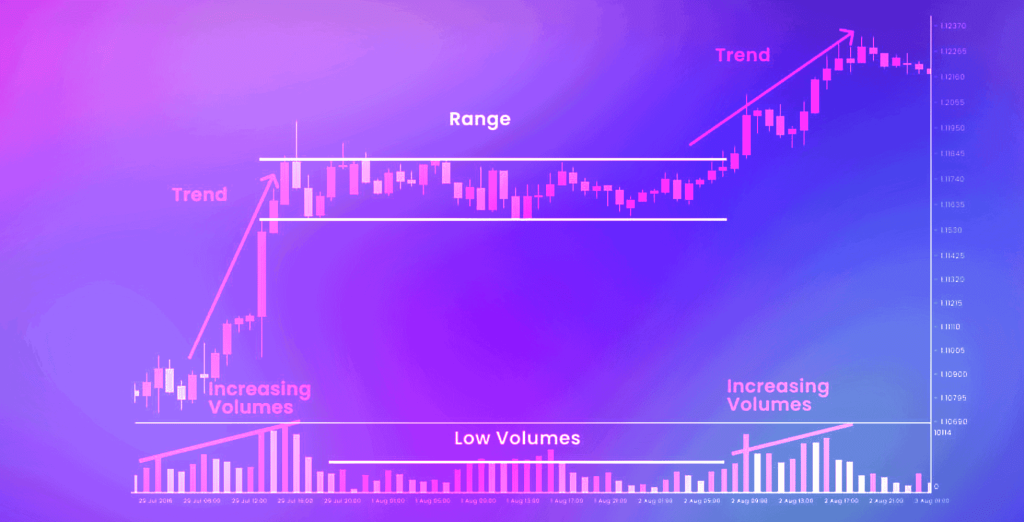
正しくインジケーターのカウントが機能しない典型的な例が、以下のようなレンジ相場です。

本来は細かく波をカウントする必要がないこのようなレンジ相場であっても、インジケーターではカウントがされてしまうのです。

ただし、トレンド相場だと以下のように正しくカウントされる傾向にあります。

したがって、機能しやすい相場と機能しづらい相場を見極めつつ、あくまで参考程度に活用することがフィボナッチ関連のインジケーターを使いこなすためのコツです。

エリオット波動のインジケーターをトレードで活用する方法

エリオット波動を使ったトレードでは、第3波を狙うことがポイントです。

第3波はトレンドの中盤に現れるので他の波と比べて見つけやすく、かつ5つの推進波の中でも最も値幅を狙える波なのです。

したがって、第3波を集中的に狙うことでリスクリワードの高い取引が可能になります。

インジケーターを使えば第3波を狙うことは、そう難しくありません。

上昇トレンドの場合は、第2波がカウントされた時点で、第2波の安値を損切り位置として買いエントリーをします。

そして、フィボナッチを使って第3波がどこまで伸びるのかを予測して、そのレートに利益確定目標を設定するだけです。

また上記のようなチャートだと、これまで続いた下落トレンドラインも上にブレイクしているのでより強い上昇トレンドシグナルとなります。

エリオット波動を使ってFintokeiに挑戦する

Fintokeiとは、個人トレーダーがプロトレーダーに挑戦する場を提供しているプロップファームです。

Fintokeiでは、デモ環境を使って仮想資金を運用していき、損失率を抑えつつ、一定以上の利益率を達成することでプロトレーダーになることができます。

Fintokei公認のプロトレーダーになると、デモ口座における取引利益額をもとにデータ提供料として報酬がトレーダーへ支払われます。

初期の取引資金や価格が異なる豊富なプランがFintokeiでは用意されており、最低1万円台からプロトレーダーへの挑戦を始められるのです。

今回紹介したエリオット波動を活用した取引手法は、Fintokei公認のプロトレーダーになるために役立つでしょう。

また、動画の学習コンテンツが用意されていたり、ブログでトレードの基礎知識が学べたりとトレーダーへの教育に力を入れている点もFintokeiの強みです。

無料トライアルも実施していますので、ぜひFintokeiのサービスを体験してみてください。

Fintokeiについては、以下の記事で詳しく解説しているのでぜひ参考にしてください。

≫プロップファームFintokeiとは？おすすめする理由や始め方を紹介！

まとめ

この記事では、エリオット波動の基本概念やそのカウントの難しさ、そしてインジケーターを活用することでその問題を解決する方法について詳しく解説しました。

エリオット波動のカウントを正確に行うためにはトレードスキルや経験が必要となるので、プロトレーダーでもリアルタイムで100％正確に行うことは困難です。

そこでインジケーターを活用すると、100％正しいとは言えないもののカウントの精度を高められ、エントリーやエグジットのタイミングを見極めやすくなります。

今回紹介した3つのインジケーターを活用し、自分のトレードスタイルに合ったものを選びましょう。

慣れてきたら、フィボナッチ比率や他のテクニカル分析手法と組み合わせて、より高度なトレード戦略を実践してみてください。